Notebook for Assignment 7

Author

Aki Vehtari et al.

1 General information

This assignment relates to Lecture 7 and Chapter 5.

We recommend using JupyterHub (which has all the needed packages pre-installed).

Reading instructions:

General Instructions for Answering the Assignment Questions
  • Questions below are exact copies of the text found in the MyCourses quiz and should serve as a notebook where you can store notes and code.
  • We recommend opening these notebooks in the Aalto JupyterHub, see how to use R and RStudio remotely.
  • For inspiration for code, have a look at the BDA R Demos and the specific Assignment code notebooks
  • Recommended additional self study exercises for each chapter in BDA3 are listed in the course web page. These will help to gain deeper understanding of the topic.
  • Common questions and answers regarding installation and technical problems can be found in Frequently Asked Questions (FAQ).
  • Deadlines for all assignments can be found on the course web page and in MyCourses.
  • You are allowed to discuss assignments with your friends, but it is not allowed to copy solutions directly from other students or from internet.
  • Do not share your answers publicly.
  • Do not copy answers from the internet or from previous years. We compare the answers to the answers from previous years and to the answers from other students this year.
  • Use of AI is allowed on the course, but the most of the work needs to by the student, and you need to report whether you used AI and in which way you used them (See points 5 and 6 in Aalto guidelines for use of AI in teaching).
  • All suspected plagiarism will be reported and investigated. See more about the Aalto University Code of Academic Integrity and Handling Violations Thereof.
  • If you have any suggestions or improvements to the course material, please post in the course chat feedback channel, create an issue, or submit a pull request to the public repository!
if (!require(tidybayes)) {
    install.packages("tidybayes")
    library(tidybayes)
}
Loading required package: tidybayes
if (!require(brms)) {
    install.packages("brms")
    library(brms)
}
Loading required package: brms
Loading required package: Rcpp
Loading 'brms' package (version 2.22.0). Useful instructions
can be found by typing help('brms'). A more detailed introduction
to the package is available through vignette('brms_overview').

Attaching package: 'brms'
The following objects are masked from 'package:tidybayes':

    dstudent_t, pstudent_t, qstudent_t, rstudent_t
The following object is masked from 'package:stats':

    ar
if (!require(metadat)) {
  install.packages("metadat")
  library(metadat)
}
Loading required package: metadat
if(!require(cmdstanr)){
    install.packages("cmdstanr", repos = c("https://mc-stan.org/r-packages/", getOption("repos")))
    library(cmdstanr)
}
Loading required package: cmdstanr
This is cmdstanr version 0.8.1
- CmdStanR documentation and vignettes: mc-stan.org/cmdstanr
- CmdStan path: /home/runner/.cmdstan/cmdstan-2.35.0
- CmdStan version: 2.35.0
cmdstan_installed <- function(){
  res <- try(out <- cmdstanr::cmdstan_path(), silent = TRUE)
  !inherits(res, "try-error")
}
if(!cmdstan_installed()){
    install_cmdstan()
}

2 Simulation warm-up

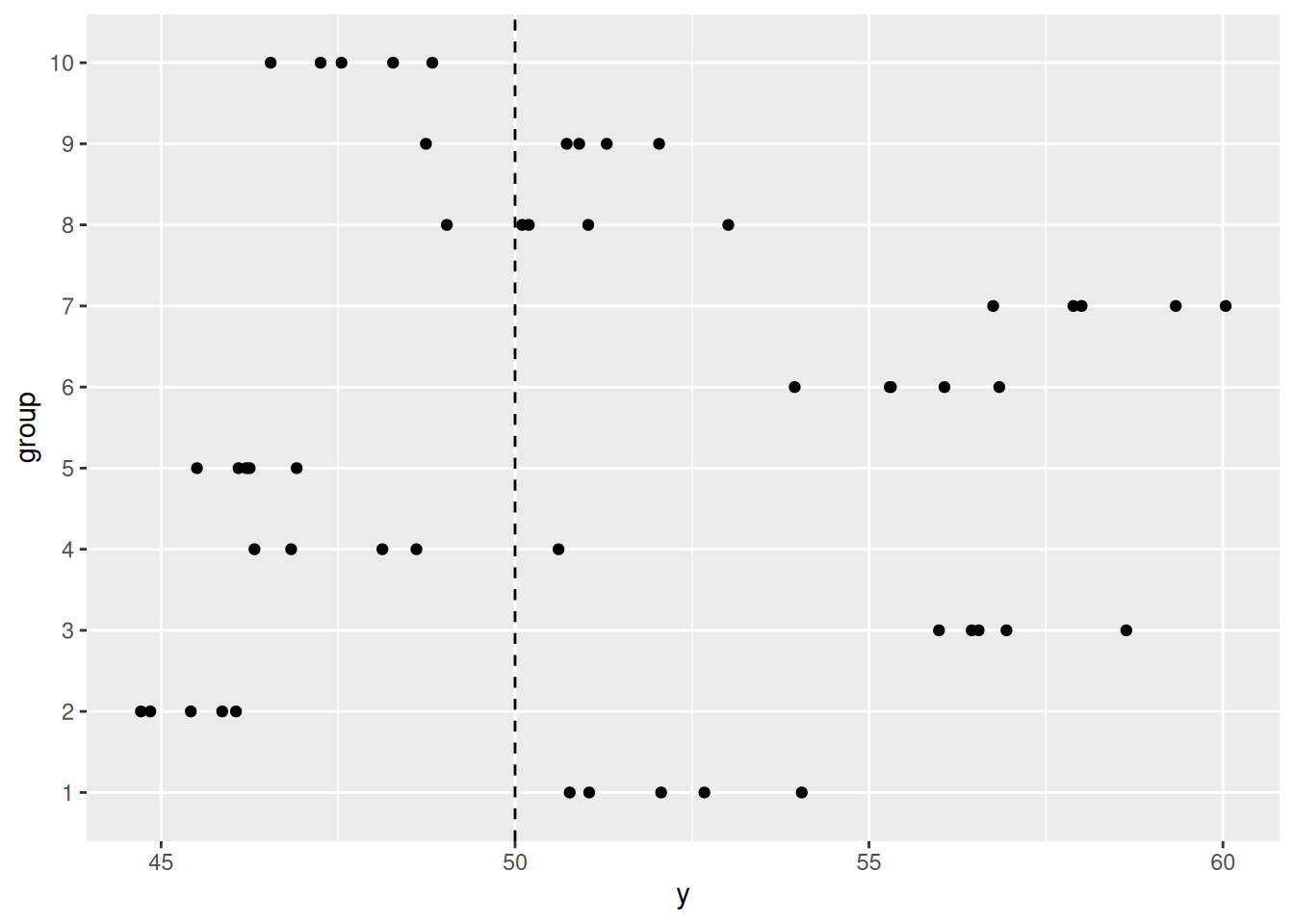
Here is the function to simulate and plot observations from a hierarchical data-generating process.

hierarchical_sim <- function(group_pop_mean,
                             between_group_sd,
                             within_group_sd,
                             n_groups,
                             n_obs_per_group
                             ) {
  # Generate group means
  group_means <- rnorm(
    n = n_groups,
    mean = group_pop_mean,
    sd = between_group_sd
  )

  # Generate observations

  ## Create an empty vector for observations
  y <- numeric()
  ## Create a vector for the group identifier
  group <- rep(1:n_groups, each = n_obs_per_group)
  
  for (j in 1:n_groups) {
    ### Generate one group observations
    group_y <- rnorm(
      n = n_obs_per_group,
      mean = group_means[j],
      sd = within_group_sd
    )
    ### Append the group observations to the vector
    y <- c(y, group_y)
  }

  # Combine into a data frame
  data <- data.frame(
    group = factor(group),
    y = y
  )

  # Plot the data
  ggplot(data, aes(x = y, y = group)) +
    geom_point() +
    geom_vline(xintercept = group_pop_mean, linetype = "dashed")
}

Example using the function:

hierarchical_sim(
  group_pop_mean = 50,
  between_group_sd = 5,
  within_group_sd = 1,
  n_groups = 10,
  n_obs_per_group = 5
  )
Error in ggplot(data, aes(x = y, y = group)): could not find function "ggplot"

3 Sleep deprivation

The dataset sleepstudy is available by using the command data(sleepstudy, package = "lme4")

Below is some code for fitting a brms model. This model is a simple pooled model. You will need to fit a hierarchical model as explained in the assignment, but this code should help getting started.

Load the dataset

data(sleepstudy, package = "lme4")
Error in find.package(package, lib.loc, verbose = verbose): there is no package called 'lme4'

Specify the formula and observation family:

sleepstudy_pooled_formula <- bf(
  Reaction ~ 1 + Days,
  family = "gaussian",
  center = FALSE
)

We can see the parameters and default priors with

get_prior(pooled_formula, data = sleepstudy)

We can then specify the priors:

(sleepstudy_pooled_priors <- c(
  prior(
    normal(400, 100),
    class = "b",
    coef = "Intercept"
  ),
  prior(
    normal(0, 50),
    class = "b",
    coef = "Days"
  ),
  prior(
    normal(0, 50),
    class = "sigma"
  )
))

And then fit the model:

sleepstudy_pooled_fit <- brm(
  formula = pooled_formula,
  prior = pooled_priors,
  data = sleepstudy
)

We can inspect the model fit:

summary(pooled_fit)

4 School calendar

Meta-analysis models can be fit in brms. When the standard error is known, the se() function can be used to specify it.

The dataset dat.konstantopoulos2011 has the observations for the school calendar intervention meta-analysis.

data(dat.konstantopoulos2011, package = "metadat")

As mentioned in the assignment instructions, a unique identifier for school needs to be created by combining the district and school:

schoolcalendar_data <- dat.konstantopoulos2011 |>
  dplyr::mutate(
    school = factor(school),
    district = factor(district),
    district_school = interaction(district, school, drop = TRUE, sep = "_")
  )

Then the models can be fit

schoolcalendar_pooled_formula <- bf(
  formula = yi | se(sqrt(vi)) ~ 1,
  family = "gaussian"
)  

schoolcalendar_pooled_fit <- brm(
  formula = schoolcalendar_pooled_formula,
  data = schoolcalendar_data
)

Predictions for a new school can be made using the posterior_epred function:

new_school <- data.frame(
  school = factor(1),
  district = factor(1),
  district_school = factor("1_1"),
  vi = 0 # the expectation of the prediction is not affected by the sampling variance, so this can be any number
)
  

schoolcalendar_post_epred <- posterior_epred(
    schoolcalendar_pooled_fit,
    newdata = new_school,
    allow_new_levels = TRUE
  )

It can be helpful to plot the posterior estimates. Here is a function that will do this:

plot_school_posteriors <- function(fit, dataset) {
  tidybayes::add_predicted_draws(dataset, fit) |>
    ggplot(
      aes(
        x = .prediction,
        y = interaction(district, school, sep = ", ", lex.order = TRUE))) +
    tidybayes::stat_halfeye() +
    ylab("District, school") +
    xlab("Posterior effect")
}

And can be used as follows:

plot_school_posteriors(
  fit = schoolcalendar_pooled_fit,
  dataset = school_calendar_data
)