The exercises here refer to the lecture 1/BDA chapter 1 content, not the course infrastructure quiz. This assignment is meant to test whether or not you have sufficient knowledge to participate in the course. The first question checks that you remember basic terms of probability calculus. The second exercise checks you recognise the most important notation used throughout the course and used in BDA3. The third-fifth exercise you will solve some basic Bayes theorem questions to check your understanding on the basics of probability theory. The 6th exercise checks on whether you recall the three steps of Bayesian Data Ananlysis as mentioned in chapter 1 of BDA3. The last exercise walks you through an example of how we can use models to generate distributions for outcomes of interest, applied to a setting of a simplified Roulette table.
This quarto document is not intended to be submitted, but to render the questions as they appear on Mycourses to be available also outside of it. The following will set-up markmyassignment to check your functions at the end of the notebook:
library(markmyassignment)
assignment_path = paste("https://github.com/avehtari/BDA_course_Aalto/",
"blob/master/tests/assignment1.yml", sep="")
set_assignment(assignment_path)Assignment set:
assignment1: Bayesian Data Analysis: Assignment 1
The assignment contain the following (3) tasks:
- p_red
- p_box
- p_identical_twinIf you use pen and paper, it may help to draw pictures as follows (see also assignment_instructions#fig-workflow):
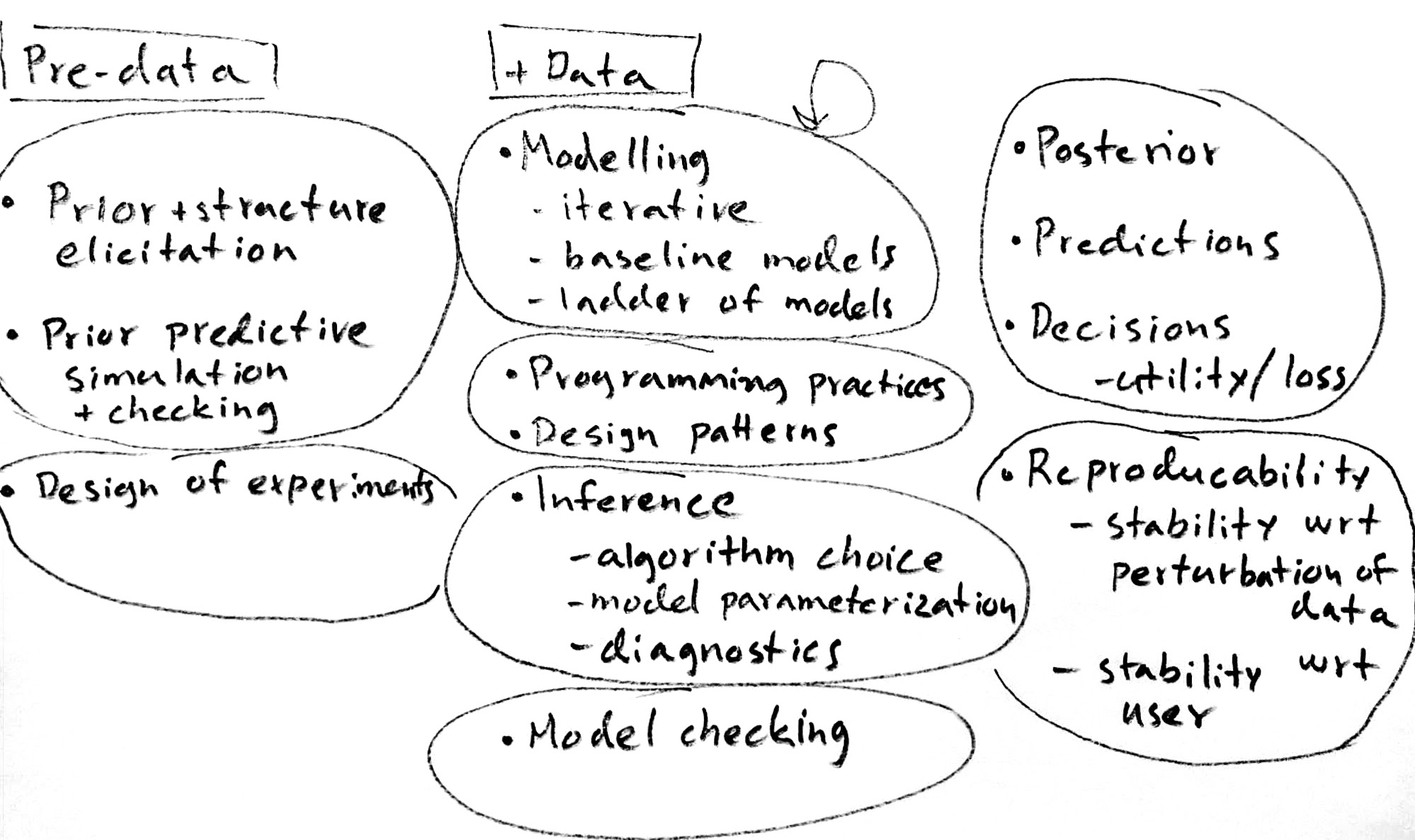
See Figure 1 for illustration of parts of Bayesian workflow.
The following will help you implementing a function to calculate the required probabilities for this exercise. Keep the below name and format for the function to work with markmyassignment:
boxes_test <- matrix(c(2,2,1,5,5,1), ncol = 2,
dimnames = list(c("A", "B", "C"), c("red", "white")))
p_red <- function(boxes) {
# Do computation here, and return as below.
# This is the correct return value for the test data provided above.
0.3928571
}
p_box <- function(boxes) {
# Do computation here, and return as below.
# This is the correct return value for the test data provided above.
c(0.29090909,0.07272727,0.63636364)
}The R functions below might help you calculating the requited probabilities.
Keep the below name and format for the function to work with markmyassignment:
Incomplete code can be found below.
# Ratio of red/black
theta <- # declare probability parameter for the binomial model
# Sequence of trials
trials <- seq(#start value of sequence,#end value of sequence,#value for spacing)
# Number of simulation draws from the model
nsims <- # number of of simulations from the binomial model
# Helper function for getting the ratios
binom_gen <- function(trials,theta,nsims){
df <- as.data.frame(rbinom(nsims,trials,theta)/trials) |> mutate(nsims = nsims,trials = trials)
colnames(df) <- c("Ratios","Nsims","Trials")
return(df)
}
# Create a data frame containing the draws for each number of trials
ratio_60 <- do.call(rbind, lapply(trials, binom_gen, theta, nsims)) # lapply applies elements in trials column to binom_gen function, which is then rowbound via do.callNow plot a histogram of the computed ratios for 10, 50 and 1000 trials, using the code below
Suppose you are now certain that theta = 0.6, plot the probability density given 1000 trials using the code below.
size = # number of trials
prob = # probability of success
binom_data <- data.frame(
Success = 0:size,
Probability = dbinom(0:size, size = size, prob = prob)
)
ggplot(binom_data, aes(x = Success, y = Probability)) +
geom_point() +
geom_line() +
labs(title = "PMF of Binomial Distribution", x = "Number of Successes", y = "PDF")The following will check the functions for which markmyassignment has been set up:
✔ | F W S OK | Context
⠏ | 0 | task-1-subtask-1-tests
⠏ | 0 | p_red()
✖ | 1 3 | p_red()
────────────────────────────────────────────────────────────────────────────────
Failure ('test-task-1-subtask-1-tests.R:21:3'): p_red()
p_red(boxes = boxes) not equivalent to 0.5.
1/1 mismatches
[1] 0.393 - 0.5 == -0.107
Error: Incorrect result for matrix(c(1,1,1,1,1,1), ncol = 2)
────────────────────────────────────────────────────────────────────────────────
⠏ | 0 | task-2-subtask-1-tests
⠏ | 0 | p_box()
✖ | 1 3 | p_box()
────────────────────────────────────────────────────────────────────────────────
Failure ('test-task-2-subtask-1-tests.R:19:3'): p_box()
p_box(boxes = boxes) not equivalent to c(0.4, 0.1, 0.5).
3/3 mismatches (average diff: 0.0909)
[1] 0.2909 - 0.4 == -0.1091
[2] 0.0727 - 0.1 == -0.0273
[3] 0.6364 - 0.5 == 0.1364
Error: Incorrect result for matrix(c(1,1,1,1,1,1), ncol = 2)
────────────────────────────────────────────────────────────────────────────────
⠏ | 0 | task-3-subtask-1-tests
⠏ | 0 | p_identical_twin()
✖ | 2 3 | p_identical_twin()
────────────────────────────────────────────────────────────────────────────────
Failure ('test-task-3-subtask-1-tests.R:16:3'): p_identical_twin()
p_identical_twin(fraternal_prob = 1/100, identical_prob = 1/500) not equivalent to 0.2857143.
1/1 mismatches
[1] 0.455 - 0.286 == 0.169
Error: Incorrect result for fraternal_prob = 1/100 and identical_prob = 1/500
Failure ('test-task-3-subtask-1-tests.R:19:3'): p_identical_twin()
p_identical_twin(fraternal_prob = 1/10, identical_prob = 1/20) not equivalent to 0.5.
1/1 mismatches
[1] 0.455 - 0.5 == -0.0455
Error: Incorrect result for fraternal_prob = 1/10 and identical_prob = 1/20
────────────────────────────────────────────────────────────────────────────────
══ Results ═════════════════════════════════════════════════════════════════════
── Failed tests ────────────────────────────────────────────────────────────────
Failure ('test-task-1-subtask-1-tests.R:21:3'): p_red()
p_red(boxes = boxes) not equivalent to 0.5.
1/1 mismatches
[1] 0.393 - 0.5 == -0.107
Error: Incorrect result for matrix(c(1,1,1,1,1,1), ncol = 2)
Failure ('test-task-2-subtask-1-tests.R:19:3'): p_box()
p_box(boxes = boxes) not equivalent to c(0.4, 0.1, 0.5).
3/3 mismatches (average diff: 0.0909)
[1] 0.2909 - 0.4 == -0.1091
[2] 0.0727 - 0.1 == -0.0273
[3] 0.6364 - 0.5 == 0.1364
Error: Incorrect result for matrix(c(1,1,1,1,1,1), ncol = 2)
Failure ('test-task-3-subtask-1-tests.R:16:3'): p_identical_twin()
p_identical_twin(fraternal_prob = 1/100, identical_prob = 1/500) not equivalent to 0.2857143.
1/1 mismatches
[1] 0.455 - 0.286 == 0.169
Error: Incorrect result for fraternal_prob = 1/100 and identical_prob = 1/500
Failure ('test-task-3-subtask-1-tests.R:19:3'): p_identical_twin()
p_identical_twin(fraternal_prob = 1/10, identical_prob = 1/20) not equivalent to 0.5.
1/1 mismatches
[1] 0.455 - 0.5 == -0.0455
Error: Incorrect result for fraternal_prob = 1/10 and identical_prob = 1/20
[ FAIL 4 | WARN 0 | SKIP 0 | PASS 9 ]